Dado un conjunto de datos, podemos, a priori, querer obtener respuestas a preguntas clave para nuestro negocio a partir de su análisis:
- ¿Cuáles son los factores que más influyen en la productividad de mis empleados?
- ¿Puedo predecir la pérdida o ganancia de una oportunidad de negocio en mi empresa?
- ¿Qué probabilidad tengo de una parada en mi cadena de producción?
Antes de profundizar en el tema de este post y para que podaís conocer información básica sobre tipos de análisis de datos, os recomiendo la lectura del artículo El nivel de madurez de las organizaciones en el análisis de datos donde mi compañero Iván Toda explica, entre otras ideas, por qué el dato se ha convertido en la mejor materia prima de las empresas.
Por esta razón, antes de aplicar técnicas de análisis detallado, debemos cuestionarnos si tenemos dicha materia prima necesaria para obtener las respuestas adecuadas.
Durante esta fase el usuario se familiariza con el conjunto: se describen los datos en cuanto a estructura, tamaño y tipología y distribución de las variables. Este primer análisis es conocido como análisis descriptivo.
Tipos de datos
Este primer ejercicio de detectar tanto el número de variables de las que se dispone como su tipo es esencial. Dependiendo de los tipos de datos de los que se disponen, se podrán determinar las técnicas de análisis que mejor se ajusten a dichos datos. La clasificación de las variables según la tipología de los datos es la siguiente:
- Categórica:
- Dicotómica: puede tomar únicamente dos valores, que pueden traducirse en 0 y 1. A veces aparecen denominadas como variables tipo marca. Por ejemplo: hombre/mujer.
- Nominal: son variables numéricas cuyos valores representan una categoría o identifican un grupo de pertenencia. Por ejemplo: los colores.
- Ordinal: representan también valores pertenecientes a una categoría. La diferencia con una variable nominal es que en este caso los valores pueden ordenarse en una escala. Por ejemplo: dolor leve/moderado/fuerte.
- Numérica:
- Discreta: son variables numéricas que tienen un número contable de valores entre dos valores cualesquiera. Por ejemplo: número de habitantes en una ciudad.
- Continua: variable numérica que puede tomar cualquier valor dentro de un intervalo de valores. Es muy importante conocer las unidades en las que se mide. Ejemplo: altura de una persona.
Representación gráfica
Se dice que «una imagen dice más que mil palabras», un dicho que adquiere especial relevancia a la hora de analizar un conjunto de datos.
Algunos tipos de representaciones son las siguientes:
- Gráfico de sectores: este gráfico circular es utilizado para representar las proporciones en las que aparece un determinado valor con respecto al total. Las variables que se representan mediante este tipo de gráficos son las categóricas.
- Histogramas: este tipo de representación da una idea de la distribución de datos que toma una variable. Por ejemplo, podemos observar si la distribución de valores de los datos se ajusta a una distribución normal teórica (como se puede observar en la imagen al pie). La utilización de histogramas es necesaria a la hora de graficar variables continuas.
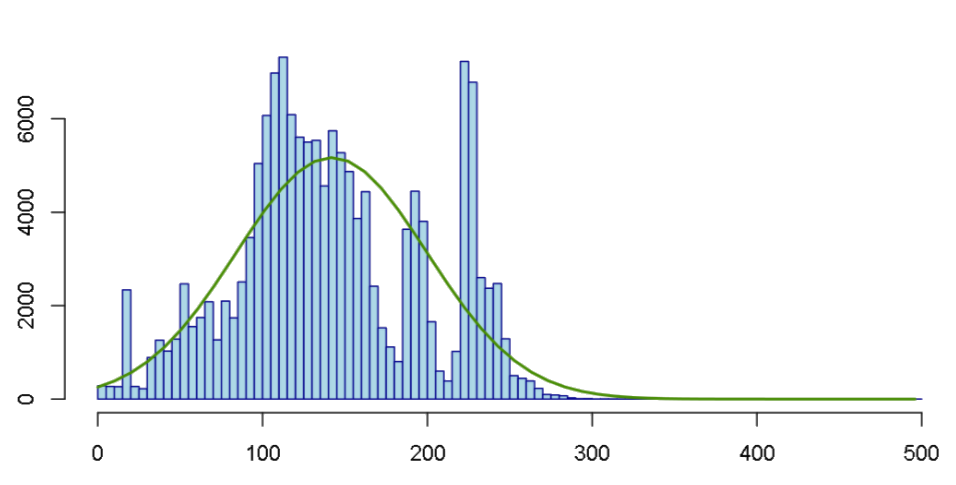
Línea verde: distribución normal teórica que mejor se ajusta a los datos.
- Gráfico de barras: este gráfico representa las proporciones en las que aparece un determinado valor, sin estar necesariamente reflejado sobre un total. Se utiliza sobre todo para representar variables categóricas.
- Gráfico de línea: este tipo de gráfico representa evolución en los datos. Principalmente es útil a la hora de representar variables de tipo continuo de las que se dispone de valores a lo largo del tiempo.
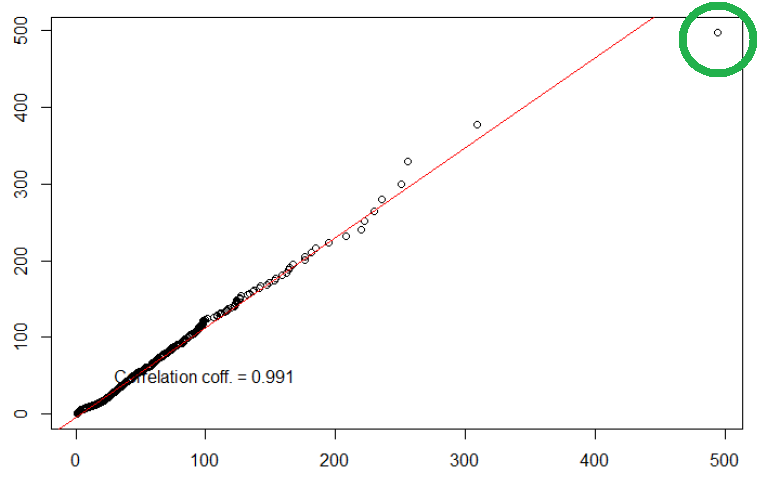
Detección y tratamiento de valores atípicos
Los valores atípicos o anomalías son aquellos que destacan de forma clara del resto por ser valores muy poco frecuentes, como, por ejemplo, los valores que son muy altos o demasiado bajos.
Estos valores pueden ser ocasionados por errores en la entrada o recogida de los datos, o pueden proceder de lecturas reales que, en efecto, están sucediendo. Normalmente estos valores se excluyen de los análisis, ya que distorsionan los resultados.
Las técnicas más utilizadas, a la par de intuitivas, son las relativas al cálculo de distancias entre los distintos datos, puesto que la idea de ser un punto distinto a los demás equivale a ser un punto distante a los demás.
Detección y tratamiento valores perdidos
También es importante detectar si existen valores perdidos. Conocer la naturaleza de las lecturas perdidas (fallo de lectura del aparato, desconexión de la red wi-fi, etc.) puede ser de ayuda a la hora de decidir qué hacer con esta pérdida de datos.
No siempre la mejor opción es retirarlos del análisis, ya que pueden ser útiles en algunos casos a la hora de extraer información, o simplemente el hecho de retirarlos restringe demasiado el tamaño del conjunto de datos.
Estadísticos básicos
Medidas de posición
El objetivo de estos estadísticos es resumir la información en cuanto a dónde (en torno a qué valor) se sitúan los datos.
Para ver cómo se calcula cada uno de ellos vamos a poner un ejemplo práctico. Supongamos que tenemos el siguiente conjunto de datos con las alturas de los miembros de una familia medidos en metros:
(1.75, 1.62, 1.62, 0.96, 1.43)
-
- Media aritmética. Se obtiene a partir de la suma de todos los valores dividida entre el número de sumandos.
-
- Mediana: 1.62. Si ordenamos los valores de nuestro conjunto de datos es el que toma la posición central.
-
- Moda: 1.62. Es el valor que se repite con mayor frecuencia en una distribución de datos.
Medidas de dispersión
Una vez que ya se conoce en torno a qué valores se encuentran los datos, debemos preguntarnos: ¿cuánto se mueven respecto a dichos valores? Para ello, existen una serie de estadísticos conocidos como medidas de dispersión. El objetivo de estos estadísticos es resumir la información en cuanto a la variabilidad.
Seguimos con el ejemplo de la familia:
- Rango: es el intervalo en el cual se mueven los datos, es decir, el definido por los valores mínimo y máximo de nuestro conjunto.
[0.96, 1.75]
- Varianza: en general, se define como la esperanza del cuadrado de la diferencia de la variable con respecto a su media.
- Desviación típica: viene dada por la raíz cuadrada de la varianza.
Es durante este primer análisis exploratorio donde se empiezan a reflejar las relaciones más evidentes existentes entre las distintas observaciones, así como posibles errores en la entrada de los datos.
Esta primera fuente de conocimiento es la que permite seguir indagando en los datos mediante análisis matemáticos más rigurosos. En definitiva, no se puede extraer valor de un conjunto de datos sin conocerlo previamente.
Si queréis ampliar información sobre los distintos tipos de analítica de datos que existen y cómo aplicarlos a vuetsra empresa o negocio, podéis descargaros la grabación de los siguientes webinars:
Watson Analytics: Analiza y predice los datos de tu negocio
Analítica predictiva: Magia o realidad ¿podemos predecir el futuro?
IBM Watson: herramientas para el análisis cognitivo y el análisis predictivo
Artículo redactado por Lidia Orellana
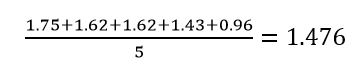


Deja una respuesta
Lo siento, debes estar conectado para publicar un comentario.